Irisan atau Interseksi - Selamat Datang Di Kumpulan Materi Matematika SMP,SMA,SMK sebagai media pembelajaran sobat semua, Pada sharing Materi Matematika kali ini yang berjudul Irisan atau Interseksi, akan kami sampaikan secara lengkap dan lugas sesuai kebutuhan pembelajaran anda. mudah-mudahan isi postingan materi matematika yang saya tulis ini dapat anda pahami. okelah, ini dia pembahasannya.

Materi :
judul : Irisan atau Interseksi

Irisan atau Interseksi

Irisan atau Interseksi

        Irisan himpunan A dan B adalah himpunan yang anggotanya merupakan persekutuan dari himpunan A dan himpunan B. Dapat pula dikatakan bahwa irisan himpunan A dan B adalah himpunan yang anggota-anggotanya merupakan anggota yang sama dari himpunan A dan himpunan B.

        Notasi irisan himpunan adalah ∩. Irisan himpunan A dan B ditulis A ∩ B, dengan A ∩ B = {x|x ∈ A dan x ∈ B}. Bila dinyatakan dalam diagram Venn, irisan dua himpunan dapat digambarkan dalam arsiran sebagai berikut.

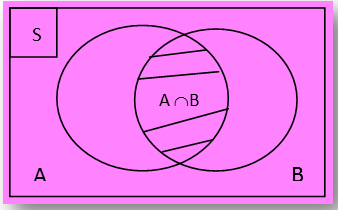
Agar kalian lebih memahaminya, perhatikan contoh-contoh berikut ini.

Contoh 1:

Diketahui dua himpunan yaitu

A = {3, 4, 5, 6, 8, 9}

B = {2, 3, 4, 7, 8, 10}

tentukan penyelesaian dari A ∩ B.

Penyelesaian:

Perhatikan anggota-anggota pada himpunan A dan B. Manakah yang anggotanya sama? Ayo kamu teliti sejenak. Ternyata anggota yang sama pada dua himpunan adalah 2, 4, 8. Jadi,
A ∩ B = {3, 4, 8}.

Contoh 2:

Diketahui dua himpunan yaitu

E = {x ∈ bilangan bulat| 4 < x <12}

F = himpunan bilangan asli kurang dari 10

tentukan anggota-anggota dari E ∩ F .

Penyelesaian:

E = {x ∈ bilangan bulat| 4 < x < 12} maka E = {5, 6, 7, 8, 9 10, 11}

F = himpunan bilangan asli kurang dari 10 maka F = {1, 2, 3, 4, 5, 6, 7, 8, 9}

Perhatikan anggota-anggota pada himpunan E dan F. Carilah anggota yang sama di kedua himpunan tersebut. Sudahkah kalian temukan? Ternyata anggota yang sama pada dua himpunan tersebut adalah 5, 6, 7, 8, 9. Jadi, E ∩ F = {5, 6, 7, 8, 9}.

Contoh 3:

Diketahui tiga himpunan sebagai berikut.

G = himpunan bilangan genap antara 10 dan 20

H = himpunan bilangan asli kelipatan 4 kurang dari 17

I = himpunan bilangan asli kelipatan 3 kurang dari 22

tentukan anggota-anggota dari G ∩ H ∩ I.

Penyelesaian:

G = himpunan bilangan genap antara 10 dan 20 maka G = {12,14, 16, 18}

H = himpunan bilangan asli kelipatan 4 kurang dari 17 maka H = {4, 8, 12, 16}

I = himpunan bilangan asli kelipatan 3 kurang dari 22 maka I = {3, 6, 9, 12, 15, 18, 21}

Untuk mencari anggota G ∩ H ∩ I, perhatikan dari ketiga himpunan tersebut, anggota yang sama pada himpunan G, H dan I adalah 12. Jadi, G ∩ H ∩ I = {12}.
baca juga Rumus Geometri Dimensi Dua

Demikianlah pembahasan Irisan atau Interseksi

mengenai Irisan atau Interseksi, mudah-mudahan bisa memberi manfaat untuk anda semua. baiklah, sekian postingan tentang materi matematika kali ini.

Anda sedang membaca artikel Irisan atau Interseksi dan artikel ini url permalinknya adalah https://matematikapasti-bisa.blogspot.com/2016/01/irisan-atau-interseksi.html Semoga artikel ini bisa bermanfaat.

Tweet